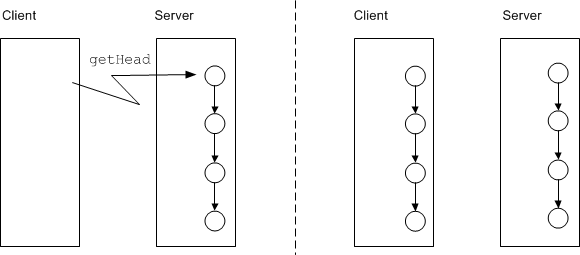
Class version of
Link before and after calling getHead.
Classes can be self-referential.
For example:
{zcode:slice}
class Link {
SomeType value;
Link next;
};
{zcode} |
This looks very similar to the self-referential interface example, but the semantics are very different. Note that value and next are data members, not operations, and that the type of next is Link (not Link*). As you would expect, this forms the same linked list arrangement as the Link interface in Self-Referential Interfaces: each instance of a Link class contains a next member that points at the next link in the chain; the final link's next member contains a null value. So, what looks like a class including itself really expresses pointer semantics: the next data member contains a pointer to the next link in the chain.
You may be wondering at this point what the difference is then between the Link interface in Self-Referential Interfaces and the Link class shown above. The difference is that classes have value semantics, whereas proxies have reference semantics. To illustrate this, consider the Link interface from Self-Referential Interfaces once more:
{zcode:slice}
interface Link {
idempotent SomeType getValue();
idempotent Link* next();
};
{zcode} |
Here, getValue and next are both operations and the return value of next is Link*, that is, next returns a proxy. A proxy has reference semantics, that is, it denotes an object somewhere. If you invoke the getValue operation on a Link proxy, a message is sent to the (possibly remote) servant for that proxy. In other words, for proxies, the object stays put in its server process and we access the state of the object via remote procedure calls. Compare this with the definition of our Link class:
{zcode:slice}
class Link {
SomeType value;
Link next;
};
{zcode} |
Here, value and next are data members and the type of next is Link, which has value semantics. In particular, while next looks and feels like a pointer, it cannot denote an instance in a different address space. This means that if we have a chain of Link instances, all of the instances are in our local address space and, when we read or write a value data member, we are performing local address space operations. This means that an operation that returns a Link instance, such as getHead, does not just return the head of the chain, but the entire chain, as shown:

Class version of Link before and after calling getHead.
On the other hand, for the interface version of Link, we do not know where all the links are physically implemented. For example, a chain of four links could have each object instance in its own physical server process; those server processes could be each in a different continent. If you have a proxy to the head of this four-link chain and traverse the chain by invoking the next operation on each link, you will be sending four remote procedure calls, one to each object.
Self-referential classes are particularly useful to model graphs. For example, we can create a simple expression tree along the following lines:
{zcode:slice}
enum UnaryOp { UnaryPlus, UnaryMinus, Not };
enum BinaryOp { Plus, Minus, Multiply, Divide, And, Or };
class Node {};
class UnaryOperator extends Node {
UnaryOp operator;
Node operand;
};
class BinaryOperator extends Node {
BinaryOp op;
Node operand1;
Node operand2;
};
class Operand extends Node {
long val;
};
{zcode} |
The expression tree consists of leaf nodes of type Operand, and interior nodes of type UnaryOperator and BinaryOperator, with one or two descendants, respectively. All three of these classes are derived from a common base class Node. Note that Node is an empty class. This is one of the few cases where an empty base class is justified. (See the discussion on empty interfaces; once we add operations to this class hierarchy, the base class is no longer empty.)
If we write an operation that, for example, accepts a Node parameter, passing that parameter results in transmission of the entire tree to the server:
{zcode:slice}
interface Evaluator {
long eval(Node expression); // Send entire tree for evaluation
};
{zcode} |
Self-referential classes are not limited to acyclic graphs; the Ice run time permits loops: it ensures that no resources are leaked and that infinite loops are avoided during marshaling.